轨道六根数（Orbital Elements，又称开普勒轨道根数）是描述一个天体（如人造卫星、行星、彗星等）在二体问题（仅受中心天体引力作用）下绕行轨道的六个独立参数。这六个数唯一确定了轨道的形状、大小、空间朝向以及天体在轨道上的具体位置。

简单说：只要知道这六个数，就能精确算出卫星在未来任意时刻的位置和速度。

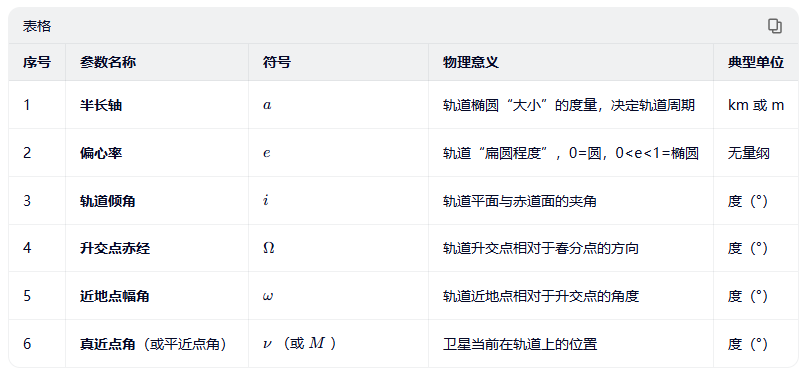
注：第6个参数有时用平近点角$M$M （需结合时间解开普勒方程求真近点角），但最终目的是确定位置。

参数分类

半长轴和偏心率决定轨道的大小和形状；

倾角、升交点赤经、近地点辐角决定轨道相对于地球的方位；

真近点角，用于计算卫星在轨道上的位置。

1半长轴

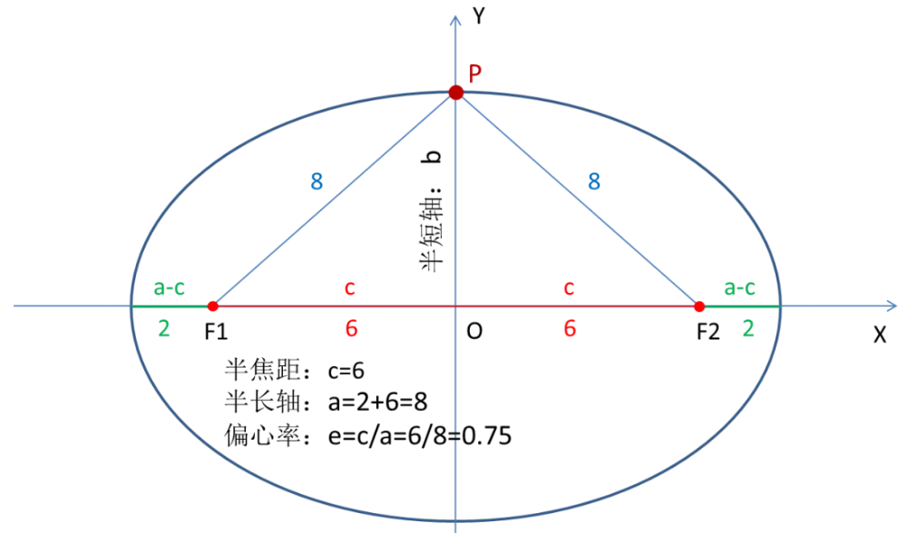
2偏心率

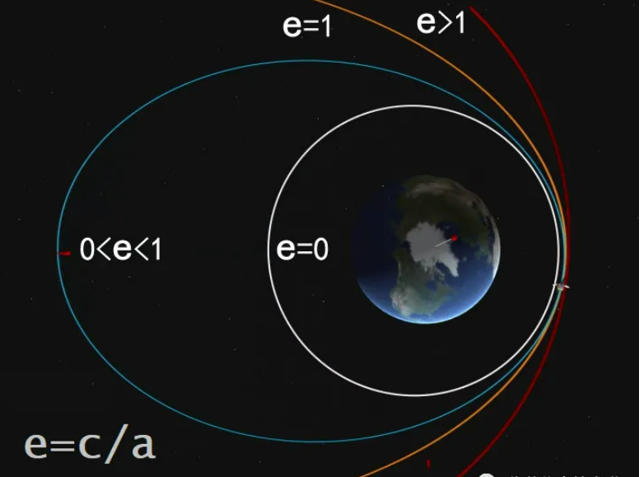
3轨道倾角

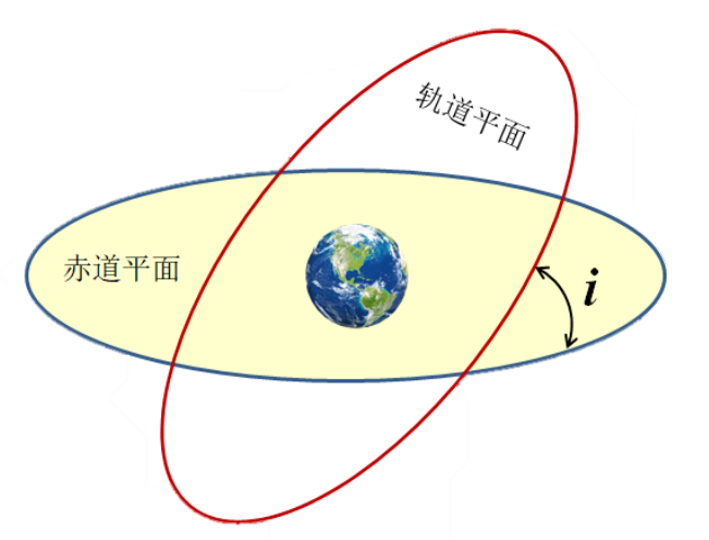
轨道倾角 $i$ 是轨道角动量矢量与地球自转轴（或赤道平面法向）之间的夹角，也可以理解为轨道平面相对于赤道平面的“倾斜程度”。

，通常用i表示。从这个参数能看出卫星是顺行还是逆行。

• 分类：
  • $i=0^{\circ }$i=0∘ ：赤道轨道（顺行）；
  • $0^{\circ }<i<{90}^{\circ }$0∘<i<90∘ ：顺行轨道（与地球自转同向）；
  • $i={90}^{\circ }$i=90∘ ：极地轨道；
  • ${90}^{\circ }<i<{180}^{\circ }$90∘<i<180∘ ：逆行轨道；
  • $i={180}^{\circ }$i=180∘ ：赤道逆行轨道。

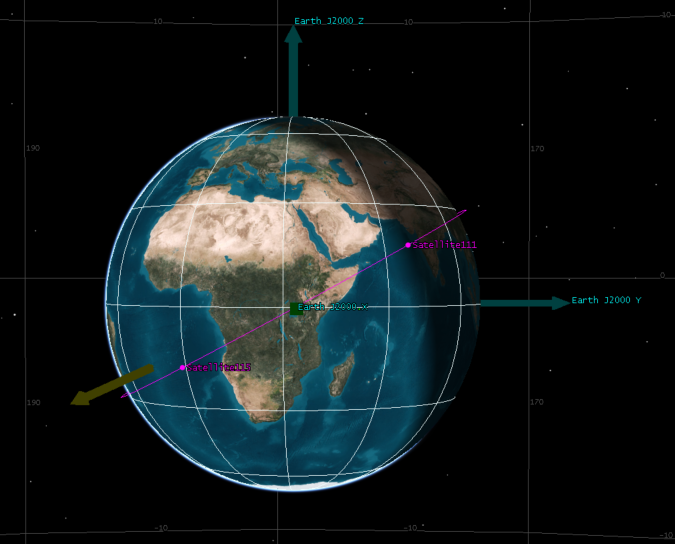
4 升交点赤经RAAN（Right Ascension of the Ascending Node）

再次复习下“春分点”与“黄道面”

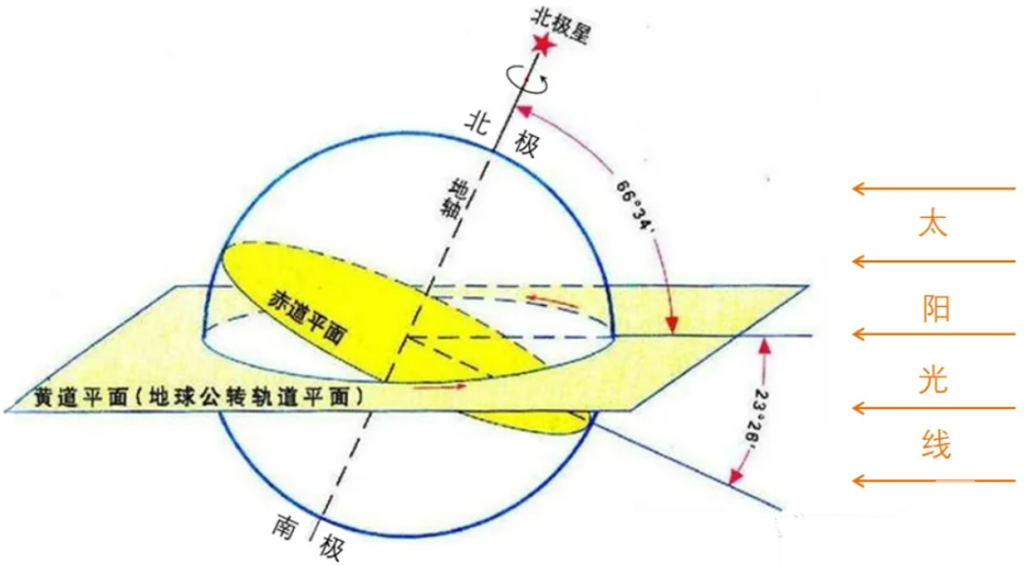
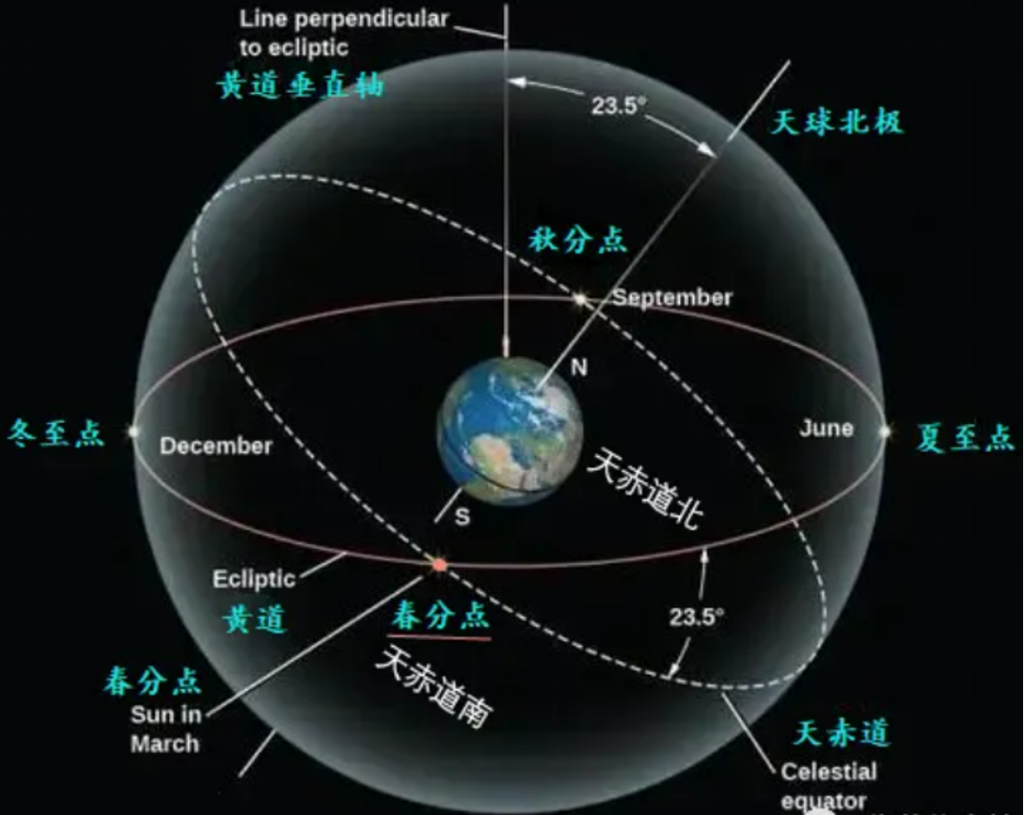
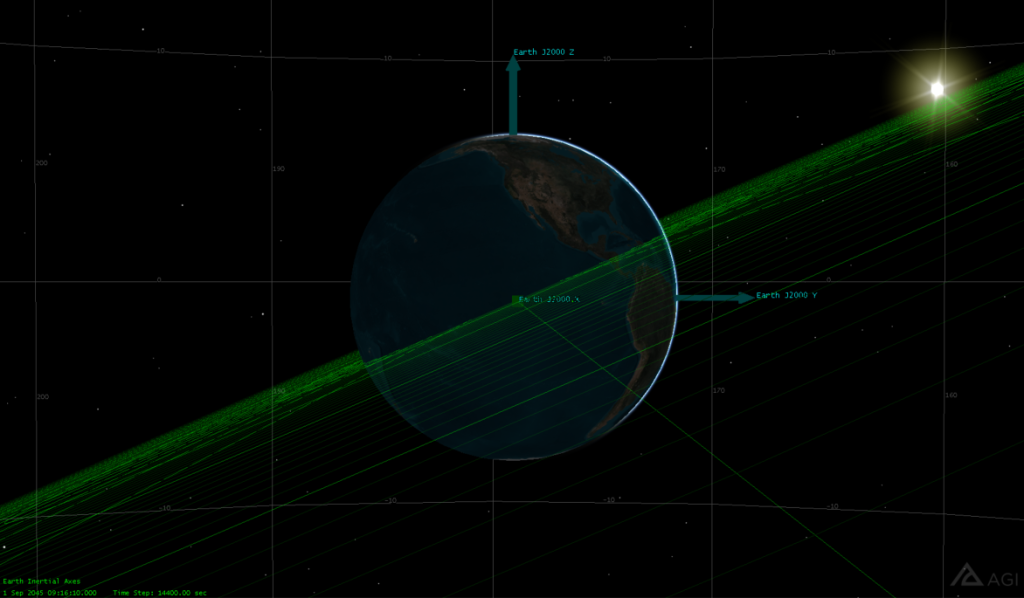
升交点：

升交点（ascending node ）就是卫星从地球的南半球向北半球飞行时经过地球赤道平面的那个点。（轨道面与赤道面的另一个交点称为降交点。）

升交点赤经：卫星轨道的升交点与春分点之间的角距。

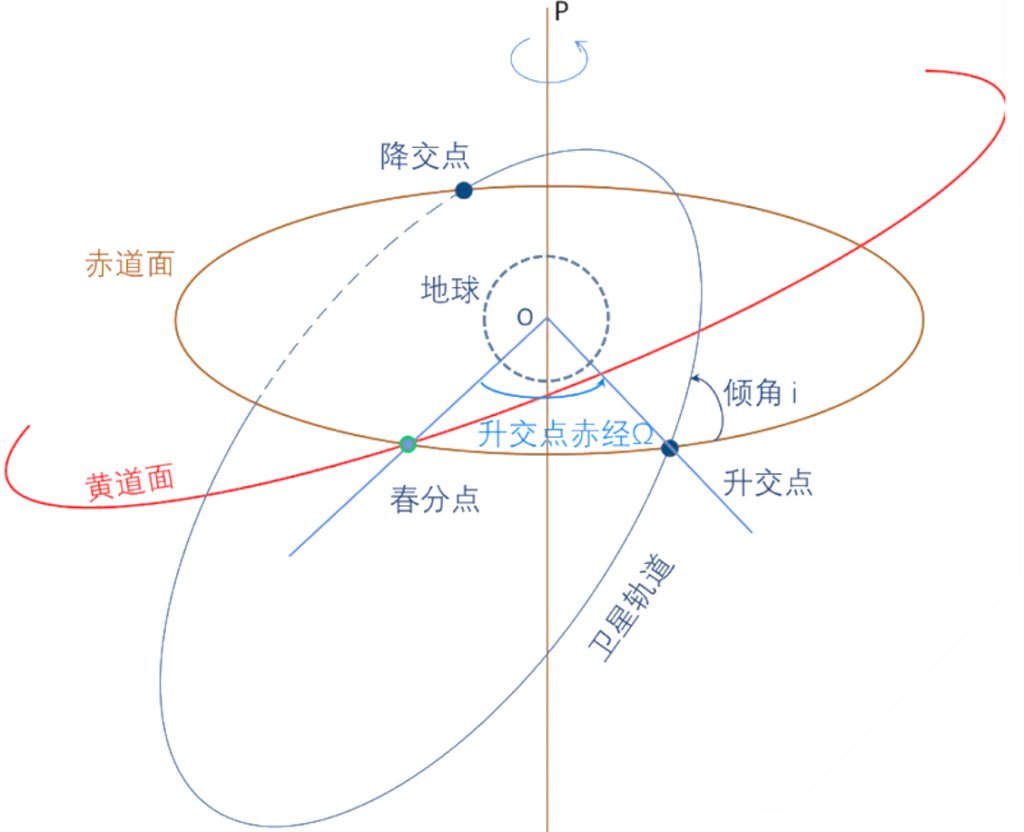
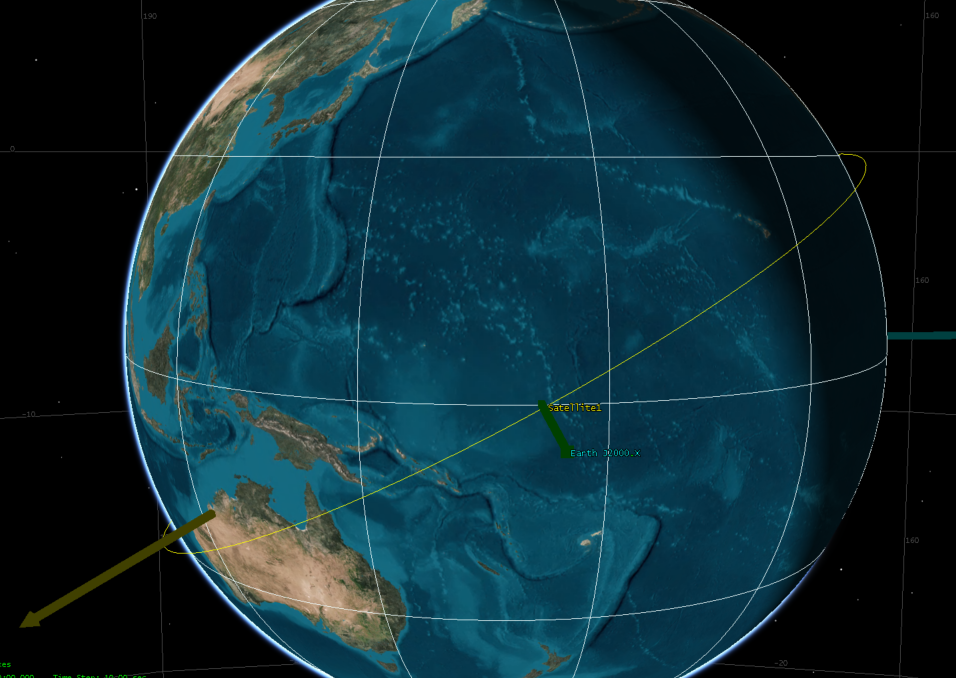
升交点赤经0度的情况：卫星轨道面与赤道的交点，J2000的X轴（从地球质心指向春分点），这两个看起来重合了。

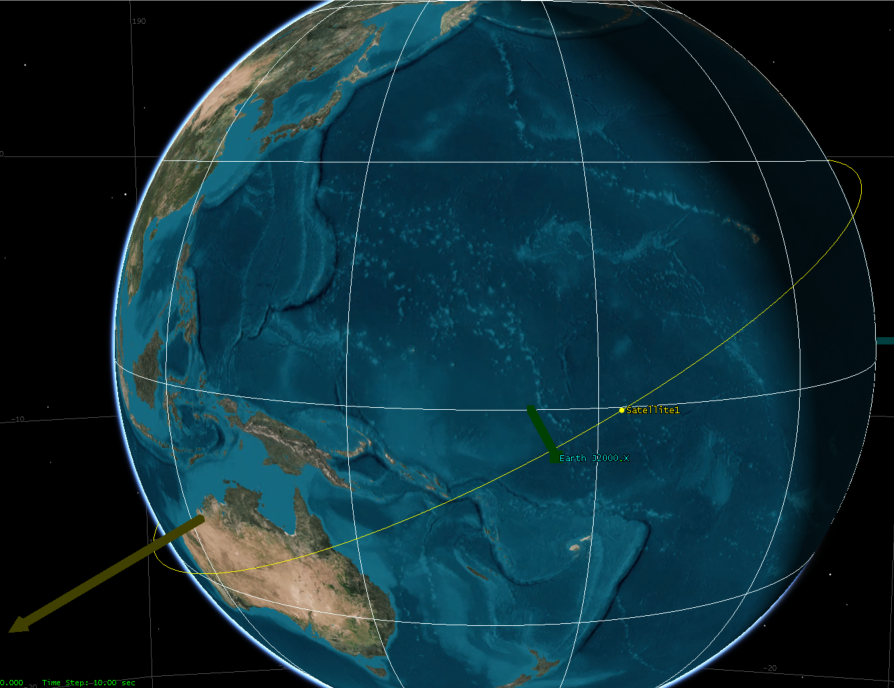
升交点赤经10度的情况

5 近地点幅角

近地点与远地点：

卫星在轨道上运行时，离地球最近的点称为近地点(Perigee)，最远的点称为远地点(apogee)。

从轨道升交点到近地点之间以地心为顶点的张角就是所谓近地点幅角(argument of perigee)，通常用ω表示。近地点幅角是在轨道平面。近地点幅角决定了椭圆轨道在轨道平面内的方位。

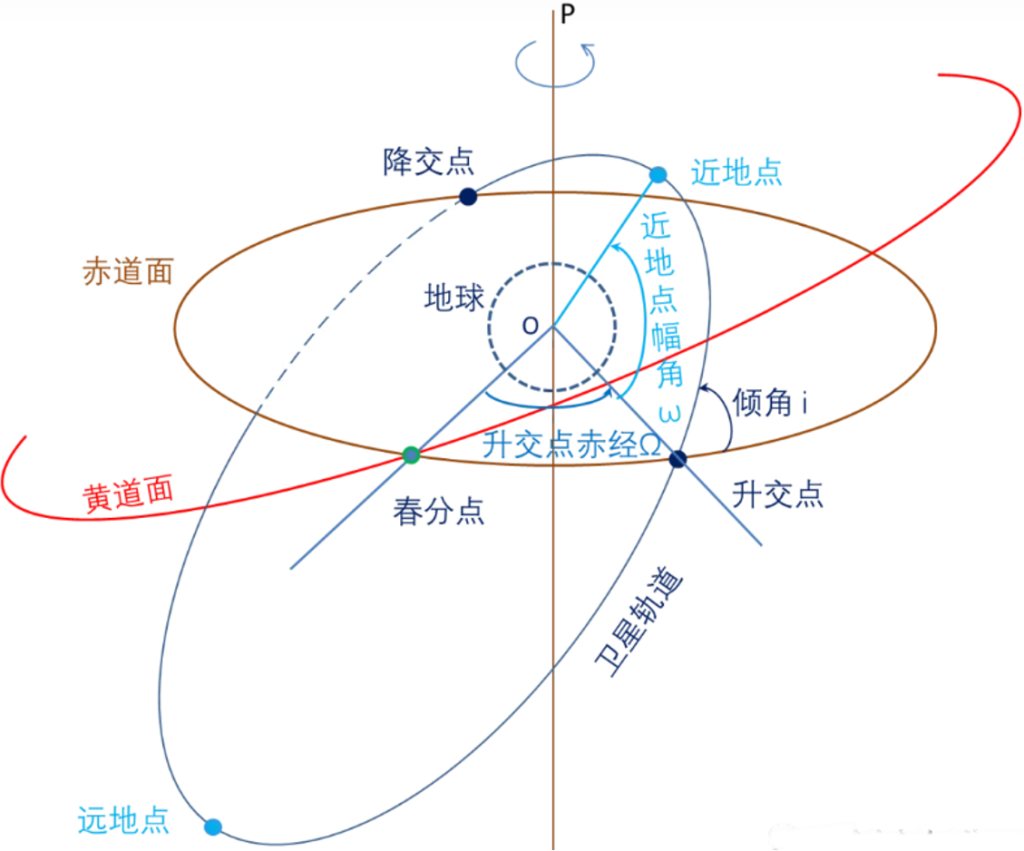
近地点幅角是0度的情况（其他5个参数一样）：

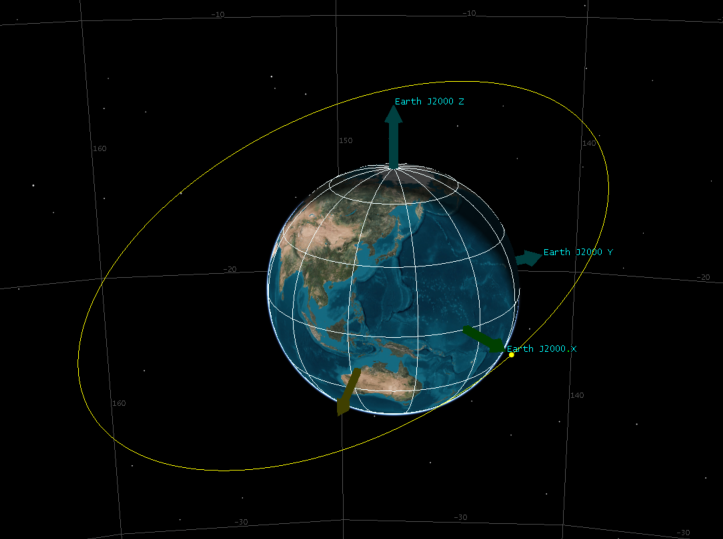
近地点幅角是90度的情况（其他5个参数一样）：

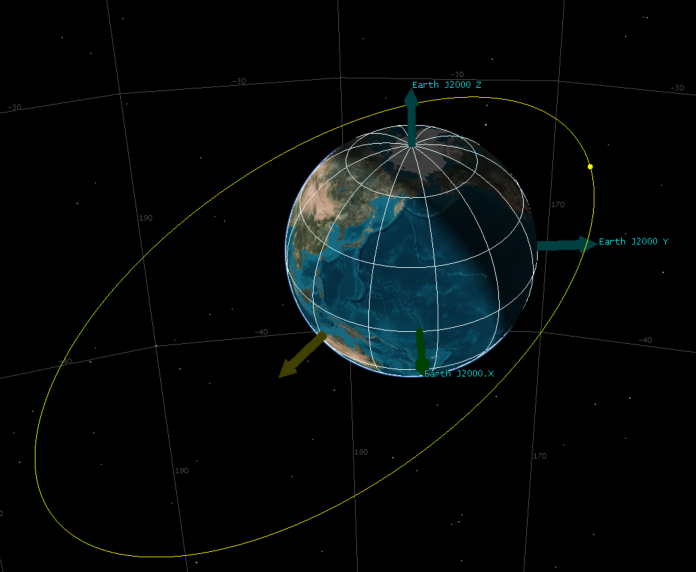
近地点幅角是270度的情况（其他5个参数一样）：

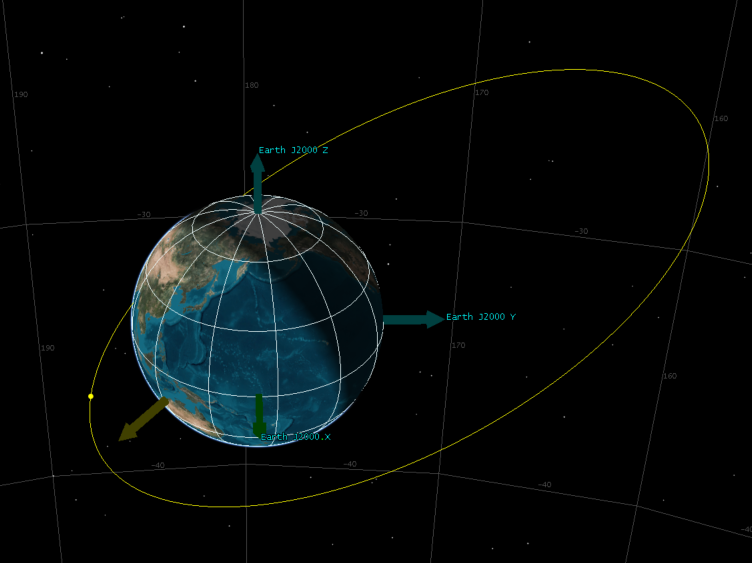
6 真近点角

• 常用形式有三种：
  1. 真近点角（True Anomaly, νν ）：从近地点到卫星当前位置的中心角（在轨道平面上测量）；
  2. 平近点角（Mean Anomaly, MM ）：基于平均角速度计算的等效角度，便于时间推算；
  3. 过近地点时刻（Time of Perigee Passage, tptp​ ）：卫星上一次经过近地点的精确时间。
• 说明：这三者可通过开普勒方程相互转换。

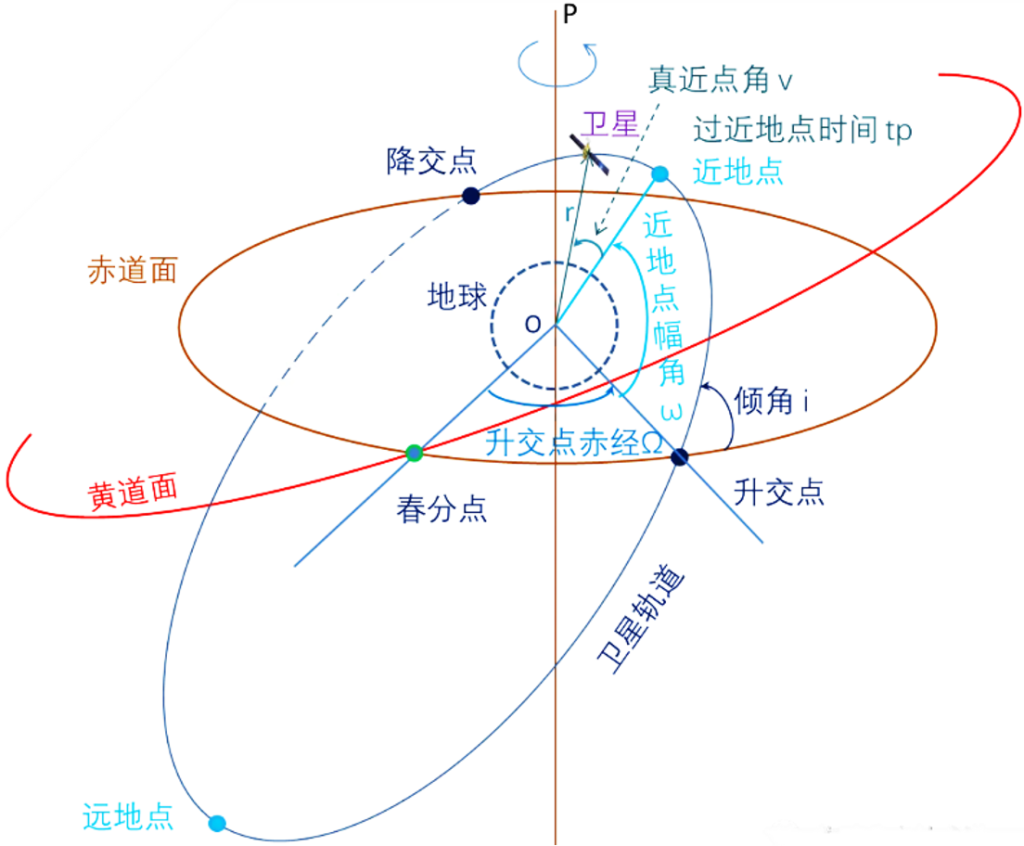
真近点角决定了卫星在轨道中的具体位置。

注意事项：

可能有人会有疑问：“假设一个卫星的轨道倾角是60度，那么卫星不是可以正向绕地球公转也可以反向吗？那么六根数如何确定卫星是正向运行还是反方向运行尼？”

解答：一旦你固定了轨道倾角为 60°，并且采用标准的轨道根数定义（特别是结合“升交点”和“近地点幅角”等参数），那么卫星的运行方向就已经确定了——只能是顺行（自西向东）。
如果它反向运行（自东向西），那它的轨道倾角就不再是 60°，而是 120°。看轨道参数的话，升交点已经变了。